Introduction :
Have you ever asked yourself a question, Why do we need to study mathematics since childhood? In my case, I asked this question to myself a lot of times! One such time I thought why do we need numbers more precisely mathematical numbers in the first place? What is the use case of mathematical number systems in our real world? Do we really need all those numbers that we have learned so far since our primary schooling? Let’s figure out the answers to all these questions together and in this process, we will understand the beauty of mathematics and how it will make our life easier in the real world.
Mathematics the language of science :
Have you ever imagined our real world, without numbers? Numbers are everywhere, right? it is helpful in our daily day-to-day activities. What is the actual use of these numbers in our real world?
Mathematics numbers are just a representation tool that conveys information without the use of a language model that mankind knows. It also conveys the same information that the language model portrays, with as minimum effort as possible. For example, let’s imagine a case where you need to know the distance between two places. How do you represent this distance, without numbers? You may tell the distance in your language(e.g. twenty kilometers).
This representation may seem long and difficult to understand for somebody, who doesn’t know your language. For that purpose, we need a simple yet more versatile tool to convey the information. That’s where mathematical numbers play an important role. Instead of saying the distance in the language model, we developed a simple yet versatile tool called mathematical numbers. We all know that mathematics is the language of science. Now using the number system, we can say the distance is (20km). We can use these mathematical numbers to model our real world in a simple way.
Real-world scenario of mathematical numbers :
I hope, now you may get a basic point for one of the main purposes of the mathematical numbers. If you do not, then consider another situation, Let’s imagine, If you are going to buy some groceries in the supermarket, for instance, you need to buy some apples. How do you know, how much Apple you want? Well, you may want 2 kilograms of Apple. Now you see here, that you are quantifying Apples with numbers. Without the number system, how would you quantify the apple you want? It seems complex! right?
Now, after purchasing everything you want, you are going to the billing counter to bill what you have purchased. What do you see in the bill? You see a bill number, Items you have purchased, and price these all are some basic stuff in the bill. Here, why do we need a bill number? To maintain uniqueness among every bill in the supermarket, they give a unique identity number for each bill called a bill number. Let’s think, Without bill number, how do we differentiate every bill? Well, we may give some unique string of characters for each bill for identification, but it seems very complicated right? And it doesn’t provide any orders either.
Now you are paying cash for your purchase, right? Here, how do you equate the quantity of Apple with the required amount of money without using numbers? Well, basically I don’t know. At last the cashier, counts the money you paid.
Classification of numbers :
Mathematical numbers form the foundation of mathematics and serve to represent quantities, measure relationships, count objects, and solve problems in a wide range of fields, including science, engineering, finance, and many more. There are several different types of mathematical numbers, each with its own unique properties and applications. Numbers are everywhere, so it is essential to know about their classification and use cases.
There are so many different classifications for numbers that are possible. But, here we are going to see only the fundamental classification. The below-given diagram shows the major classification of numbers
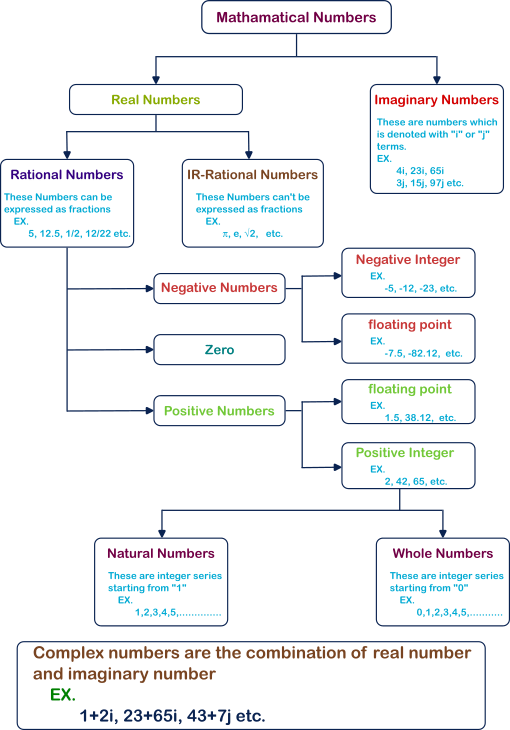
1. Real Numbers :
These are the numbers, that we needed for our smooth sailing of day-to-day activity. Without these numbers, maybe our life would be chaos!!! is there any chance the numbers are fake? then why do we name it as real numbers? You will know about it when we talk about complex numbers. It requires a separate post to explain about it. We will do it in the future. This is just an introduction post to the number system, so we just stick with the basics.
Real numbers are an essential type of mathematical number that includes all rational and irrational numbers. They are used to represent continuous quantities, such as lengths or distances, and can be represented on the number line.
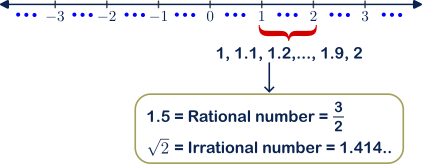
In general, we represent the Real numbers in the horizontal axis of the number line and Imaginary numbers in the vertical axis of the number line.
With these real numbers alone, we can easily simplify our day-to-day life. Let’s say,
- The tree is 50.80 m tall
- Give me a 1 L of milk.
- My salary is $ 5000.
Note :
In the mathematical domain, Real numbers are denoted as (R)
Real numbers are further classified into two main categories.
- Rational numbers
- Irrational numbers
Rational numbers :
Why do we need rational numbers in the first place? before trying to answer the question, let’s look at a practical real-world scenario. You have an apple and you need to share that apple equally with your friend. Then how much portion of apple both of you will get? well, half apple, right? But how did you represent this in a mathematical way? You may say 0.5 of apple, but by this time you don’t know about the floating point numbers, then how could you mathematically represent that?
For this, we want the rational numbers. Rational numbers are numbers, which can be written in the format of 
(fraction). From our example, we can represent the portion of the apple as 
by using rational numbers.
Rational numbers are used to represent the portions of something without the need for floating point numbers. Floating point numbers are too difficult to handle because some are convergent (numbers after the floating point have an end) and some are divergent (numbers after the floating point do not have an end). Some floating point numbers are recursive (numbers after the floating point keep on repeating) and some are non-recursive (numbers after the floating point don’t repeat). Even we can represent the recurring and non-recurring floating point numbers, approximately with the help of rational numbers.
i.e.
= 3.141592653………= 
(Approximate value)
Rational numbers can be expressed as the ratio of two integers, such as or 
. They are used to represent quantities that are not whole numbers, such as distances or amounts of time. Rational numbers are also called fractional numbers.
Examples of rational numbers
I need the half ( ) pizza
A quarter of my salary ( 
) goes to the house rent.
Note :
In the mathematical domain, Rational numbers are denoted as (Q)
Irrational numbers :
By now you know about irrational numbers, right? The numbers that can’t be represented in the manner are known to be irrational numbers. Why do we need these irrational numbers? Naturally occurring events are the sources for these irrational numbers. For example,
= a constant which presents in every circle
= the maximum possible natural rate of growth for any process
Examples of irrational numbers
= 1.4142135623730950488……..
= 3.141592653………
Now you may argue that we may represent as a rational number ( ), then how it could be an irrational number? See, is just an approximate value for and it is not the exact value, hence we can’t always represent the as a rational number .
e = 2.718281828459045…
Note :
In the mathematical domain, Irrational numbers are denoted as (I)
Classification of Rational and Irrational numbers :
Before going to the classification, just consider another example. Now, you have 5 apples out of which 3 are rotten, so you throw away those 3 rotten apples and you are left with 2 apples. But how do you represent the rotten (thrown away) apples mathematically? Well, you may say 3 apples, but it isn’t correct. Because these 3 apples are not in your hand now, how could you represent a reduction in something? This gives birth to negative(-) numbers.
Finally, you and your friend eat the remaining 2 apples. Then how could you represent this absence of the apple? the answer is pretty simple, “0” apple. That’s it, now we have a mathematical number to represent the absence of something.
- Negative numbers :
These numbers are represented with the negative sign (-) in front of the number, to represent the reduction in the value of something.
e.g.
From our Apple example,
Total apples = 5
Rotten apples (thrown away) = 3
Remaining apples = 5 + (-3) = 2
Examples of negative numbers
– 2, – 23, – , – e, – 
, etc.,
- Zero :
Zero is used to represent the absence of something in the mathematical domain.
e.g.
From our Apple example,
Apples you ate = 2
Remaining Apple = 2 + (-2) = 0
- Positive numbers :
These positive numbers are used to represent any existing quantity in the real world like height, weight, speed, count etc.,
e.g.
From our Apple example,
The total number of apples = 5 apples
Examples of positive numbers
2, 23, , e, 
, etc.,
Positive numbers and negative numbers are further classified into integers and floating-point numbers.
Floating point numbers :
Numbers in the mathematical system which have a decimal point in their notation are known to be floating-point numbers. Why do we need this? Let’s If you have pizza, you and your friend have to share it equally, then how many portions both of you will get? The answer is straightforward, right? i.e. . Instead of this rational number notation, you can say this in the floating point number as 0.5 of pizza.
An infinite number of floating-point numbers exist between the two integer values.
e.g.
In the number line, the floating numbers between the integer 5 and 6 are 5.1,5.111,5.120,………etc.,
Examples of floating point numbers
= 3.141592653………..( non repeating floating point number)
7.181818181……(repeating floating point number)
-5.1(negative floating point number)
8.2(positive floating point number)
Integer :
Another type of mathematical number is the integer, which includes both positive and negative whole numbers. Integers are used to represent quantities that can be either positive or negative, such as temperature or altitude.
In the number line, it denotes the number’s position.
Note :
In the mathematical domain, Integer numbers are denoted as (Z)
Examples of integer
1, 34, 56,100 = positive integer
-5, -27, -158 = negative integer
Integers are further classified into two major types.
i.e,
- Natural numbers :
The most common type of mathematical numbers are the natural numbers, also known as the counting numbers. These are the numbers we use to count objects or measure quantities, such as 1, 2, 3, and so on. Natural numbers can be represented on the number line and are used to denote position.
In the mathematical domain, Natural numbers are denoted as (N)
It doesn’t include number zero (“0”)
Examples of Natural numbers
N = 1, 2, 3, 4, 5, 6, 7,…….. etc.,
- Whole numbers :
The combination of natural numbers and the mathematical number zero (0) is known to be whole numbers. This included number zero (”0”).
In the mathematical domain, Whole numbers are denoted as (W)
Examples of Whole numbers
W = 0, 1, 2, 3, 4, 5, 6, 7,…….. etc.,
2. Imaginary Numbers :
This name itself reveals the nature of these numbers is imaginary. We don’t use these numbers in our daily activities, but they took a very special place in advanced mathematical numbers such as complex numbers. How could any number be imaginary? If so, why it is really important for us to consider it? Actually, these imaginary numbers have a story, and we will discuss it in the near future. But for now, just think of this as a real number with “i” (or) “j” at its beside. It paves the path for the complex numbers, that we will discuss in a future post.
In general, imaginary numbers are represented in the vertical axis of the number line.
Representation of imaginary numbers :
Imaginary numbers are represented as,
2i, 3i, 48i (or) 2j, 3j, 48j
Both representations about imaginary numbers are correct. But, don’t ever put the “i” (or) “j” term before the number, some calculator accepts imaginary numbers like this, but don’t do this in the written format.
Note :
Some textbooks refer to imaginary numbers with “i” and some textbooks refer to imaginary numbers with “j”. As my background is as an Electronics Engineer, we represent Electric Current as i, to avoid this ambiguity here we refer to imaginary numbers with “j” (i.e. 3j) for the sake of simplicity. If you are happy with the “i” notation that is also fine.
Complex numbers :
Its name only seems complex, but understanding the actual numbers isn’t complex. It is one of the most important inventions in mathematics. Complex numbers are everywhere, throughout modern science and technology. As my background is as an Electronics Engineer, without these complex numbers, we can’t represent, analyse and understand all the basic electronic signals.
It is one of the most exciting and surprising topics in mathematics to travel. So we will discuss it in future posts.
But for now, just think about it as the combination of the real numbers and the imaginary numbers. It is mathematically represented with the real numbers and the imaginary numbers separated by the addition symbol.
Mathematical representation :
Ex,
Complex number = 2 + 3j
Complex plane :
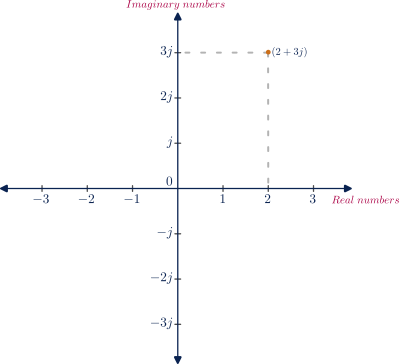
Note :
Complex numbers are generally represented as “real numbers + imaginary numbers”, but it is not wrong to switch positions of the real and the imaginary numbers, though it is not recommended.
Conclusion :
1) Real numbers (R) :
- Rational numbers (Q)
- Irrational numbers (I)
- Negative number
- zero
- Positive number
- Floating point numbers
- Integers (Z)
- Natural numbers (N)
- Whole numbers (W)
2) Imaginary numbers
Complex numbers = Real number + Imaginary number
Overall, mathematical numbers are an essential tool in the field of mathematics and have countless applications in a wide range of fields. Whether we are counting objects, measuring quantities, or solving complex problems, mathematical numbers are an indispensable part of our daily lives.